Another explanation of Quantum Mechanic

Chapter 2

In this serie of posts, I'll try to present another possible explanation of the spooky quantum mechanic effect. I'm not sure it's a theory, but feel free to comment below if you think I'm missing or misinterpreting some concepts here. I'm not aware of other people presenting these ideas, so if I'm repeating other people's concepts here, please be ensured it's completely unwillingly.

The serie is split in 3 chapters, which each chapter building on the conclusion of the previous one, so I advice you start by this first chapter.

Trying to explain some of the causes of quantum mechanic experiments is usually hard. Many physic professors will introduce wave functions (and many other mathematical tools and conventions) before you can start to grasp the observations and the theory.

In this writing, the mathematical language will be kept to a minimum in order to feel intuitive to understand.

Ok, let's start!

Dimensions

In the previous chapter, we've found that a two dimension space can be "folded" in a single dimension space by using a space filling curve. In reality, space filling curves can spread any dimension space. You can have a curve that visits all 3 dimensions or 4 dimensions:

Why is it useful here ?

Let's imagine a 2D world where the evil Dr Lockdown is trapping the Princess between 4 walls, like this:

How can the Princess exits the jail ?

The solution for us, souls living in a 3D world is obvious, we'd advice the Princess to get out of her 2D space, jumps out the 3D space (where there is no walls) and jumps back the 2D space, like this:

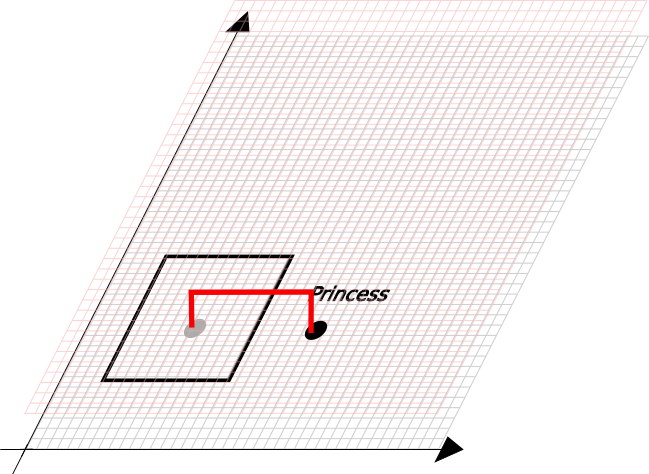
You'll say it's cheating, but I'd answer: it's thinking out of the box.

Application to Quantum Mechanics

Quantum tunneling

Let's talk about one strange QM experiment: Quantum Tunneling .

In this experiment, one particule is travelling on one direction. In this direction, a wall (some material) is preventing the particle to continue its trip. Yet, if one puts a detector for the particle after the wall, it happens that the detectors is triggered. It's like if the particle crossed the wall as if it doesn't exist.

Let's imagine now that the particle is in fact travelling on its space filling curve, and the space filling curve happens to visit a higher dimension (like in the princess example above but with 4D instead of 3D). In that case, the particle travelling on this curve has not seen the wall, it can be detected on the detector.

The usual explanation for this effect is based on the fact that the wave function of the particle is not zero after the wall, so the particle can exit/exist here. A wave function is a mathematical tool used to predit the probability to one or more characteristic of a particle. The experiment was looking at the position characteristic and the probability was non zero after the wall.

Now let's consider that the probability is just the probability of a particle to follow one specific space filling curves.

There is a small chance (non zero) that the particle is on a 4D space filling curve and if it's on this curve, then it'll skip the wall.

Casimir effect

Another strange experiment: Casimir effect

In this experiment, 2 plates are located very close to each other, forming what's called a cavity. Then a vacuum is made (to ensure it's not the medium that's falsing the experiment). The QM explains that particles could pop up into existence anywhere (including in the vacuum) with some energy. Without the apparatus, two particles of opposite phase would end up annihilating each other, so the average energy of the vacuum is equal to the electromagnetic field's energy.

With the apparatus, there is an amplication effect of the particle whose wave frequency (wavelength) is a multiple of the distance of the plate (like a guitar's string is oscillating between the two pinched point). Other particle with a different wavelength would annihilate, so only the particles with the expected wavelength are amplifying each other. These particles ends up pushing (or pulling depending on the configuration of the plate) on the plates, and a small force is measured on those.

The question is: where do the particles come from ?

If we account for a 4D space filling curve here, the particle can come from any space around (from our 3D space or the 4th dimension). The particle pops into our space whenever it's located in our dimensions. The 2 plates are obstacles preventing the particle to return to its original dimension.

The energy of the field is the average of the energy of each particle participating in the field. So, in order to keep balance, when trapping the particles here, you're voiding somewhere else particles. There is no net energy creation, the thermodynamic equilibrium is preserved.

When we were to explain statistic and probability with large set (so large that we decided we can't count the items), we could also account for a single particle here travelling on its space filling curve and sometimes visiting us. The mean (what we observe at macroscopic scale) is just the average of the particles in existence in our dimension at any given observation event.

Conclusions

Right now, the concept of a particle following a 4 (or more) dimension space filling curve is already strange, but let's think a little about the implication:

1. There is nothing explaining why the space is only using 3 dimensions. Read that sentence again. This also means that nothing justify the space only using 3 dimensions. If we are 3D creatures, can be conclude that 4D does not exits ?
2. We've observed that the 3 space dimensions we are used to are isotropic (it means that whatever the direction you take, the same physical effect happens). We could make the hypothesis that the 4th dimension is also isotropic, but there's nothing justifying this. If this dimension were not following the same laws than the lower dimensions, that could explain we don't feel this dimension at our scale.
3. Space filling curves, if they exist, must be very localized. It means that at a larger scale, they converge to straight lines (a bit like a wool thread that's a line at our scale, but that's full of multiple spirals at microscopic scale).

I'll push this concept a bit further in the next chapter.