Another explanation of Quantum Mechanic
Chapter 1
In this serie of posts, I'll try to present another possible explanation of the spooky quantum mechanic effect. I'm not sure it's a theory, but feel free to comment below if you think I'm missing or misinterpreting some concepts here. I'm not aware of other people presenting these ideas, so if I'm repeating other people's concepts here, please be ensured it's completely unwillingly.
The serie is split in 3 chapters, which each chapter building on the conclusion of the previous one, so I advice you start by this first chapter.
Trying to explain some of the causes of quantum mechanic experiments is usually hard. Many physic professors will introduce wave functions (and many other mathematical tools and conventions) before you can start to grasp the observations and the theory.
In this writing, the mathematical language will be kept to a minimum in order to feel intuitive to understand.
Ok, let's start!
Dimensions
You are usually thinking you are living in a 3rd or 4th dimensions world (depending if you account the time for a dimension, see chapter 3 for some question about this).
If I ask you what is a dimension, you'll likely think about the mathematical diagram of an axis, an origin, a bit like this:

Two dimensions ? Intuitively, you'll draw another axis, perpendicular to the first one (I will say orthogonal later on instead), like this:

As a matter of fact, what you imagine here, is the concept of manipulating 2 dimensions.
A dimension can be seen as a degree of freedom for an object of the same (or lower) dimension to evolve in its universe in some direction.
In the one dimension case above, a point could slide along the axis from any length, horizontally, but obviously can not slide in the other dimension vertically.
In order to manipulate this freedom, we select a reference point (called origin) and start to measure from it by comparing to some unit vector. In the example, above, a point could move 3 inches to the right from the origin.
We could define a dimension as a single length (or distance from the origin).
In a 2 dimensions case, you'd need 2 lengths to locate a point, with respect to some origin point, and two unit vector that are orthogonal.
I'll demonstrate that it's not always the case.
Space filling curves and fractal dimensions
Let's take the previous diagram and add 2 points: A and B.

To locate any point, intuitively, you'd use 2 coordinates (if you label your axis X and Y, you'd say A is x units of length on X and y units of length on Y).
But it's not always the case. Let's draw a spiral in there:
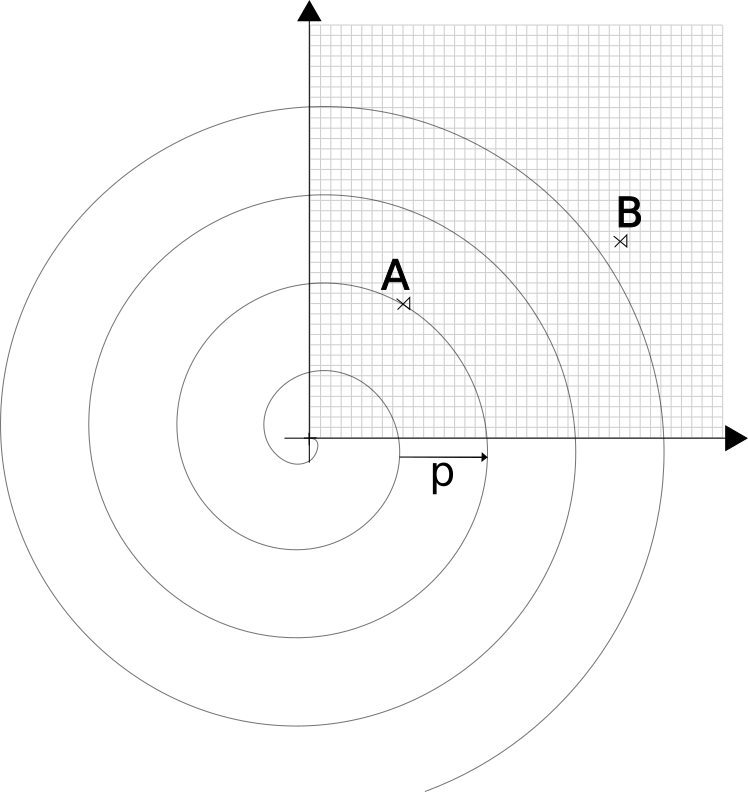
Now, you can locate the point A with a single dimension: the distance from the origin to the point along the spiral's branch. We define the curve by the spiral's pitch (that is, the distance from one branch to the next branch).
Ok you say, but you can't locate point B this way: it's not on the spiral
You are right. You'd need to adjust the pitch of the spiral to match, like this:
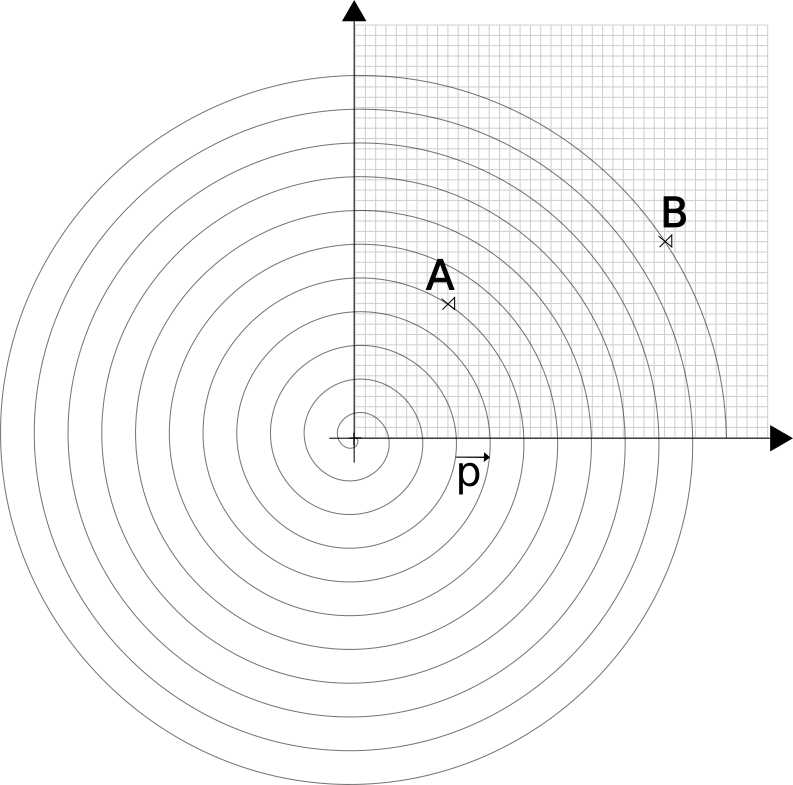
In fact, to be able to express the coordinates of all possible points in a plane, you'd need a spiral with a zero length pitch. Restrospectively, it'll also give a coordinate that's infinite for each point.
So, what you are saying is: to get one dimension from a two dimension object, you'd need infinite length?
Yes, it looks like it's going nowhere. But please follow me here. This spiral is a mathematical object called a "space filling curve". It's a curve that... fills the space.
This one is not practical but it's intuitive to understand. There are many other space filling curves (you can check Hilbert space filling curve for a good localized curve).
Now, I'll write down my first hypothesis for this theory:
Let's make the hypothesis the space is not infinitely divisible: it's quantified
If you can't divide the space indefinively, that is, at some scale, a particle can only be there or there but not in between, then it must exist a space filling curve that goes from all these points. Thus locating any particule boils down to choosing a common origin and "locating" the distance of the particle from this origin along the space filling curve.
There is a theory (called quantum loop gravity) that makes the same hypothesis.
I'm stopping here for the first chapter. In the next chapter, I'll explain why this is very important to understand some behavior of the quantum particles.