Another explanation of Quantum Mechanic
Chapter 3
In this serie of posts, I'll try to present another possible explanation of the spooky quantum mechanic effect. I'm not sure it's a theory, but feel free to comment below if you think I'm missing or misinterpreting some concepts here. I'm not aware of other people presenting these ideas, so if I'm repeating other people's concepts here, please be ensured it's completely unwillingly.
The serie is split in 3 chapters, which each chapter building on the conclusion of the previous one, so I advice you start by this first chapter.
Trying to explain some of the causes of quantum mechanic experiments is usually hard. Many physic professors will introduce wave functions (and many other mathematical tools and conventions) before you can start to grasp the observations and the theory.
In this writing, the mathematical language will be kept to a minimum in order to feel intuitive to understand.
Ok, let's start!
Randomness and probability
In the first chapter, we've found that a two dimension space can be "folded" in a single dimension space by using a space filling curve. In the second chapter, we've infered that a particle could simply follow such space filling curve that's visiting more than 3 dimensions and that could explain some strange observation of QM experiments.
There're many things that are taken for granted in numerous theory, but I'd like to reformulate them. One concept that's almost never discussed is randomness (and its counterpart: probability).
For many, randomness is a law of nature. It happens by itself and quantum mechanics just integrate it as a fundamental evidence/tool for building its concepts. Probability is the mathematical tool that's studying randomness and its effect and deduce general and valid properties for a large set of random events. QM uses probability to describe the characteristics of its objects. Thermodynamic also builds upon randomness and probability.
But the question is: what is randomness ?
At a macroscopic scale, it's easy to define it. You throw a dice or a coin and the slight variation of the environment and forces will cause large enough variation of the outcome of the characteristics of the object, enough to present observable differences.
If you were throwing a brick, you wouldn't expect the brick to flip by itself, but you would expect a small object like a coin to flip. You are, intuitively, pushing the object against some limit you might be aware of, but you don't know their exact value, like air resistance, center of gravity for the object, the elastic coefficient for your thumb muscle and so on. Randomness in this case is the product of all these informations (again, that you don't or can't measure beforehand) applied to your object.
This applies the same to many source of random as well that are used every day and constantly. You are reading this page that's encrypted by a random number generated by something the computer does not know of (like the time it takes for the next key you'll press, or some thermal measure of the CPU's diode and so on).
We can conclude that, at macroscopic level, randomness is a measure of the effects of some process/law we can't measure directly.
Quantum mechanics is the science of manipulation and characterization of randomness. Since we can't measure all the characteristics of a particle (due to Heisenberg's Uncertainty principle), we instead manipulate the probability of the characteristics. That is, we manipulate the characteristics of the randomness of the characteristics of a particle.
This is counterintuitive, because it forces us to think about where a particle could possibly be, instead of where it is, but it's very convenient to describe a complete system with enough confidence in the results.
We have to separate the alea (i.e random) to the effect of the alea (randomness), that is observing the effect of random on something: what we usually call randomness.
Yet, this doesn't explain what is randomness and from where it comes.
Let's take the conclusions of the first chapter and apply it here: what if random was the projection of a multidimensional function in our dimension ?
When we observe a particle, QM says that we collapse the wave function (in some way, we are destroying all the possibilities to fix a single measurement). That's a nice way to explain that we go from a probability to a certainty. In effect, what it means, for example on the particle position, is that from all possible position of a particle, when we observe it, we force the particle to trigger our detector, that is, be in our dimension.
This might seem complex, so I'll use an analogy here: imagine a complex number, with it's real and imaginary coordinate. When we observe this number, we'd only have access to the real axis, so we'd observe only a part of this number. Multiple observation would give more confidence in this real part, but since we can't observe the complex part (not in our dimension), we can only build probabilistic laws for the real part.
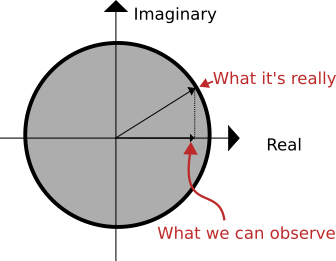
These laws will describe the effect of the complex part on the observable real part.
I proposing the idea that particles are able to move in a multiple dimensions and that randomness is the projection of the particle characteristic in our dimension. Everytime we project the random to observe it, we simply expect a particle to act in our dimension.
As a consequence, we are creatures of a lower dimension of space because of this requirement. If we were 4 or more dimensional creatures, we couldn't be fixed on a immutable observation.
That would explain the double slit experiment. In this experiment, the strangest observation consist of a single photon going through a wall with 2 slits. Behind the wall, a screen is used to observe the photon. The intuitive thinking would explain that when many photons are sent through the slit, they will either go from one slit or the other, which, in turns, direct them to specific part on the screen (2 spots following usual optic laws). Yet they are presenting an interference pattern, so it's usually explained by the particle also being a wave. They don't act like an arrow going through a window, but as a wave oscillating on the surface of a pond. Yet, if one tries to measure from which slit the photon was going through, then the interference pattern collapses.

Usual conclusions from this experiment are that photons are either wave or particle and they are only measured when they are particles. A wave would go through both slits (since it does not have a spatial location) and when detected on the screen, the particle would pop up at some predefined places: where the interference is additive (see the right part of the diagram above).
The wave is collapsing to a particle when measured. When the detector is put in the slit, the particle collapses on the detector and no interference pattern is visible. Please notice that a single photon does not show an interference pattern, it's the repeated measurement of multiple photons that show the interference pattern (a detector can only trigger for one or more photon: it's the mean of the photons position that displays the pattern).
If the wave nature of the particle is due to a higher dimensional function and that the fact of measuring the particle implies projecting the particle in our dimension, the experiment above becomes finally intuitive. In the analogy above, when being measured, we'd "observe" the projection of the random function in our real dimension, it's following some oscillation pattern due to the imaginary part stealing from the real part of the position of particle (the norm of the characteristic under measurement staying the same). The wave nature of the particle is the best function describing the oscillating spatial filling curve probability.
Time
Another concept that seems intuitive until questionned is time. We all understand what time is, but we can't describe it precisely, since when we dig into a description it triggers a hundred of new questions. All recent physic theory all struggle with the concept of time.
Is time a dimension ?
I don't think so. Intuively, we would say we can't go back in time, we can't move faster, so it's not a spatial dimension. General relativity links time with space, whatever affect the former affects the latter. At QM scale, time is usually not even considered. I think the real question is to understand what is Time.
What is the time ?
When we measure time, we measure the effect of some thermodynamic or electromagnetic process. A second is defined by the number of periods of the oscillation of a caesium-133 atom, that is, the effect of a particle in our dimension. Your watch might measure time by releasing kinetic energy or vibrating a crystal (or flowing sand, etc...) which are both thermodynamic process. You measure time like age by looking at the effect of your cells growth. In fact, time is not clearly defined. Time is an effect, not a unquestionable constant. It's impossible to measure time in a perfect ideal vacuum, you'd need a particle and observe its effect in order to know what time is.
Worst than that: time is not symmetric. You need to measure a consequence of some process, you can't measure the cause, knowing the consequence.
Down to the QM world, to observe something, you need to interact with it. That is, you need to collapse the randomness.
What if time boils down to the number of collapsing you are performing on a system?
A unobserved system would never have time flowing (that's the philosophical Berkeley's paradox). Yet, from the probability law, multiple similar system should behave the same, on average, so a unobservable system should behave the same as an observed system.
This means that a particle following a space filling curve would, on average, enters our dimension as often as an non-interacting particle.